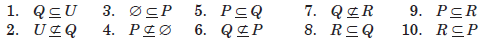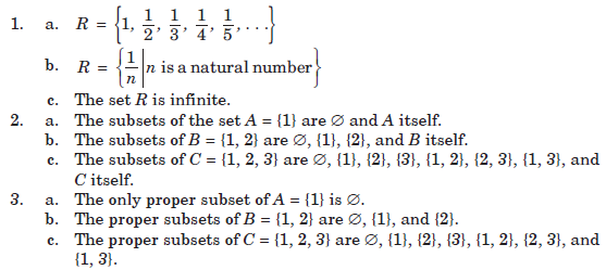Lesson 1: Basic Ideas About Sets
Textbook Pages: 2-15
Suggested Number of Hours: 8 hours
Suggested Number of Hours: 8 hours
Lesson Objectives and the K to 12 Curriculum
Learning Competencies
Learning Competencies
|
Lesson Objectives
|
Learning Competencies
|
|
• Describe, represent, and illustrate sets
• Define and illustrate equal sets and equivalent sets • Describe and illustrate the empty set and the universal set • Define subset and proper subset • Determine the cardinality of sets |
The learner describes well-defined sets, subsets, the null set, and cardinality of sets.
|
Essential Questions
How important are sets?
Technology and Resources
Math Ideas and Life Applications (MILA) 7 Textbook 2nd Edition
Materials
chalk or marker, board
Learning Plan
Introduction
To motivate the students, discuss the lesson opener on page 2 of the textbook. Then discuss the lesson under “The Notion of Sets” on pages 3 and 4. Ask them to cite their own examples of collections of objects and tell whether they are mathematical sets or not. Tell them that at the end of the lesson, they should be able to answer the essential question “How important are sets?” and support their answer.
Lesson Development
1. Define and illustrate element of a set. Write the notation for it. Discuss also the symbol for “not an element of.” Then let the students do all the items in letter B of Establishing on page 14.
2. Define and illustrate equal sets. Let the students give their own examples of equal sets.
3. Discuss the roster method and the rule method of representing a set. Point out the differences between them. Let the students have their own examples to illustrate each method.
4. Explain what is meant by finite set and equivalent sets (see pages 7–9). Have the students give their own examples to illustrate equivalent sets.
5. Define each of the following terms and give examples: empty set, universal set, and subset of a set (see pages 10–13).
6. Let the students do the exercises in letters A and C under Establishing on page 14.
Generalization and Assessment
1. Let the students do all the items under Refining on page 15.
2. Assign the exercises under Intensifying on page 15 as homework.
3. Have the students form groups of three. Have each group discuss the answer to the essential question. Ask the students to share their answer with the class afterward.
To motivate the students, discuss the lesson opener on page 2 of the textbook. Then discuss the lesson under “The Notion of Sets” on pages 3 and 4. Ask them to cite their own examples of collections of objects and tell whether they are mathematical sets or not. Tell them that at the end of the lesson, they should be able to answer the essential question “How important are sets?” and support their answer.
Lesson Development
1. Define and illustrate element of a set. Write the notation for it. Discuss also the symbol for “not an element of.” Then let the students do all the items in letter B of Establishing on page 14.
2. Define and illustrate equal sets. Let the students give their own examples of equal sets.
3. Discuss the roster method and the rule method of representing a set. Point out the differences between them. Let the students have their own examples to illustrate each method.
4. Explain what is meant by finite set and equivalent sets (see pages 7–9). Have the students give their own examples to illustrate equivalent sets.
5. Define each of the following terms and give examples: empty set, universal set, and subset of a set (see pages 10–13).
6. Let the students do the exercises in letters A and C under Establishing on page 14.
Generalization and Assessment
1. Let the students do all the items under Refining on page 15.
2. Assign the exercises under Intensifying on page 15 as homework.
3. Have the students form groups of three. Have each group discuss the answer to the essential question. Ask the students to share their answer with the class afterward.
Answer Key to Gauging What You Have Learned
Establishing
A.
1. The roster and the rule methods are the two methods of representing a set.
2. The symbol ∈ is used to denote “is an element of.”
3. The empty set or the null set is the set with no elements in it. The symbol ∅ or { } is used to denote the empty set.
4. The universal set is the set that contains all elements of all sets being considered in a specified setting. The symbol U is used to denote the universal set.
5. Two sets A and B are equal if every element of A is an element of B and every element of B is an element of A.
6. The cardinality of a finite set is the number of elements in the set.
7. The cardinality of the empty set is 0.
8. Two finite sets are equivalent if they have equal cardinalities.
9. Set A is a subset of set B if every element of A is an element of B. The symbol ⊆ is used to denote “is a subset of.”
10. The set of counting numbers is also called the set of natural numbers. This set is infinite and the symbol N is used to denote this set.
A.
1. The roster and the rule methods are the two methods of representing a set.
2. The symbol ∈ is used to denote “is an element of.”
3. The empty set or the null set is the set with no elements in it. The symbol ∅ or { } is used to denote the empty set.
4. The universal set is the set that contains all elements of all sets being considered in a specified setting. The symbol U is used to denote the universal set.
5. Two sets A and B are equal if every element of A is an element of B and every element of B is an element of A.
6. The cardinality of a finite set is the number of elements in the set.
7. The cardinality of the empty set is 0.
8. Two finite sets are equivalent if they have equal cardinalities.
9. Set A is a subset of set B if every element of A is an element of B. The symbol ⊆ is used to denote “is a subset of.”
10. The set of counting numbers is also called the set of natural numbers. This set is infinite and the symbol N is used to denote this set.
B.
|
1. 0 ∈ U
2. 6 ∈ U 3. 7 ∉ U 4. 0 ∉ P 5. 2 ∈ P |
6. 4 ∈ P
7. 0 ∈ Q 8. 2 ∈ Q 9. 5 ∉ Q 10. {2, 4} ∉ Q |
11. 1 ∉ R
12. 2 ∈ R 13. 3 ∉ R 14. 4 ∈ R 15. P ∉ R |
C.
Refining
A.
1. D = {2, 4, 6, 8, 12, 18, 24, 36, 72}
2. E = {3, 6, 9, 12, 18, 24, 36, 72}
3. F = {6, 12, 18, 24, 36, 72}
4. G = { }
5. H = {2, 3}
B.
1. D = {x ∈ U | x is a multiple of 2}
2. E = {x ∈ U | x is a multiple of 3}
3. F = {x ∈ U | x is a multiple of 2 and x is a multiple of 3}
4. G = {x ∈ U | x is a multiple of 5}
5. H = {x ∈ U | x is a prime number}
C.
1. 9
2. 8
3. 6
4. 0
5. 2
Intensifying
A.
1. D = {2, 4, 6, 8, 12, 18, 24, 36, 72}
2. E = {3, 6, 9, 12, 18, 24, 36, 72}
3. F = {6, 12, 18, 24, 36, 72}
4. G = { }
5. H = {2, 3}
B.
1. D = {x ∈ U | x is a multiple of 2}
2. E = {x ∈ U | x is a multiple of 3}
3. F = {x ∈ U | x is a multiple of 2 and x is a multiple of 3}
4. G = {x ∈ U | x is a multiple of 5}
5. H = {x ∈ U | x is a prime number}
C.
1. 9
2. 8
3. 6
4. 0
5. 2
Intensifying